El sistema numérico hexadecimal, o simplemente hexadecimal (abreviado Hex) es un sistema de numeración de base 16, es decir, para representar cualquier número se utilizan 16 dígitos los cuales son:
0, 1, 2, 3, 4, 5, 6, 7, 8 ,9, A, B, C, D, E, F
En informática para indicar que un dígito es hexadecimal se suele indicar con una H después del número, de este modo
- 2h – 2 hex – 2 hexadecimal
- 5h – 5 hex – 5 hexadecimal
Cuando el número tiene un solo dígito, se suele poner un 0 en la parte más significativa del número, de este modo
- 2h se suele escribir 02h ó 02H, también lo podrás encontrar expresado como 0x2
- 5h se suele escribir 05h ó 05H, también lo podrás encontrar expresado como 0x5
Conveniencia del sistema Hexadecimal
El sistema Hexadecimal en la informática se utiliza ampliamente por dos razones básicas:
Por la correspondencia directa entre números binarios y hexadecimales, nos permite simplificar enormemente la representación de números binarios.
Es más rápido representar y efectuar operaciones de cualquier tipo en sistema hexadecimal.
Conversión Binario – Hexadecimal
El sistema binario tiene una correspondencia directa con el sistema Hexadecimal, de modo que la conversión entre ambos sistemas es muy rápido y eficiente (a nivel de máquina), por lo que con frecuencia nos veremos representando instrucciones y otros valores en hexadecimal, en lugar de binario.
Equivalencias Binario – Hexadecimal
La equivalencia de valores binario – hexadecimal la podemos ver en la siguiente tabla:
| Hexadecimal | Binario |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Con la cual podremos realizar conversiones de forma muy rápida y simple.
Conversión de binario a hexadecimal
La base de números binarios está representada por 2 valores y la base de números Hex está representada por 16 valores. A fin de convertir un número binario en su equivalente hexadecimal:
- Dividir el número binario en grupos, cada grupo debe contener cuatro bits
- A continuación, convertir cada grupo en su equivalente hexadecimal, utiliza la tabla de conversión para obtener el resultado.
El siguiente ejemplo muestra lo sencillo que es hacer una conversión binario-hexadecimal.
Ejemplo: Convertir el número binario (1111110101110011)2 en su equivalente hexadecimal
| Binario | 1111 | 1101 | 0111 | 0011 |
| Hexadecimal | F | D | 7 | 3 |
Resultado: FD73h
Conversión de hexadecimal a binario
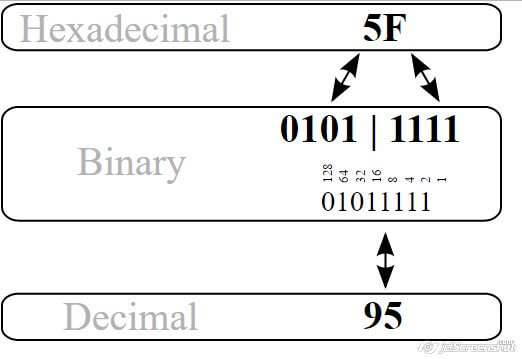
Conversión Hexadecimal – Binario
Conversión Hexadecimal a Binario
La conversión de número hexadecimal a binario es igual de trivial, pero de forma inversa:
Tomar el dígito hexadecimal individual
De la tabla de equivalencia binario-hexadecimal reemplazar por el equivalente binario
El siguiente ejemplo muestra la conversión hexadecimal a binario.
Ejemplo: Convertir el número hexadecimal (9DBA5)16 a su equivalente binario
| Hexadecimal | 9 | D | B | A | 5 |
| Binario | 1001 | 1101 | 1011 | 1010 | 0101 |
Resultado: 10011101101110100101
Representación de instrucciones de código máquina en formato hexadecimal.
Anteriormente vimos un ejemplo en el que utilizábamos algunas “instrucciones en código máquina”, recuerda que nosotros podemos definir arbitrariamente el significado de las instrucciones y es completamente válido.
| Instrucción | Significado (Definidas por el fabricante del CPU) |
|---|---|
| 0000 0000 – | No hacer nada |
| 0000 0001 – | Sumar V1 y V2 y guardar el resultado |
| 0000 0011 – | Muestra en pantalla la variable R |
| 0000 0111 – | Guarda en memoria lo que se te da en una variable llamada V1 |
| 0000 1111 – | Guarda en memoria lo que se te da en una variable llamada V2 |
| 0001 0000 – | Mover de la memoria el valor de Suma a la variable R |
| Dato | Significado (Ya sea por un estándar o por nosotros) |
|---|---|
| 0000 0001 – | 1 (el número 1) |
| 0000 0011 – | 2 (el número 2) |
| 0000 0100 – | 3 (el número 3) |
Utilizando la notación hexadecimal para las instrucciones y datos ahora tendremos:
| Instrucción | Significado (Definidas por el fabricante del CPU) |
|---|---|
| 00h – | No hacer nada |
| 01h – | Sumar V1 y V2 y guardar el resultado |
| 03h – | Muestra en pantalla la variable R |
| 07h – | Guarda en memoria lo que se te da en una variable llamada V1 |
| 0Fh – | Guarda en memoria lo que se te da en una variable llamada V2 |
| 10h – | Mover de la memoria el valor de Suma a la variable R |
| Dato | Significado (Ya sea por un estándar o por nosotros) |
|---|---|
| 01h – | 1 (el número 1) |
| 04h – | 2 (el número 2) |
| 07h – | 3 (el número 3) |
y nuestro “programa” quedará:
| Instrucción | Dato | Pseudo código |
|---|---|---|
| 07h | 01h | Guarda en la variable V1 el número 1 |
| 0Fh | 03h | Guarda en la variable V2 el número 2 |
| 01h | Realizamos la suma del valor de V1 más el valor de V2 (1 + 2, en nuestro ejemplo) | |
| 10h | Asignamos a la variable R el valor de suma (R = 3) | |
| 03h | Mostrar en pantalla la variable R | |
| 00h | No hagas nada |
El procesador leerá
0000011100000001000011110000001100000001000100000000001100000000
Nosotros leeremos:
07010F0301100300
Queda por demás claro como simplifica el formato hexadecimal la escritura y lectura de instrucciones en formato binario
Conclusiones.
Para un usuario completamente nuevo o ajeno al área de la informática a primera vista todo lo anterior parecerá mucho “rollo”, incluso para algunos del área informática, tal vez resulte conveniente mencionar que aunque no lo parezca, esta ultra compacta “iniciación” le presenta un vistazo de cómo opera a muy bajo nivel una computadora y en general, la representación de cualquier tipo de información que se manipula en las computadoras. Y es este nivel, en donde tiene su origen y su respuesta muchas de las cosas que un programador hará. Y más importante, este es el origen de cualquier sistema de cómputo por muy complejo que pueda ser.
A partir de este punto, el usuario interesado podría abordar el tema con el rigor y metodología que su especialidad le requiera.
Concluyo mencionando, una vez más, que hasta este momento se ha simplificado todo a niveles “escandalosos” para profesionales informáticos, solo resta señalar que esta introducción está orientada a usuarios no informáticos que requieren aprender a programar.
Es bueno que hayas tomado la decisión de aprender un lenguaje de programación que te permita codificar tus programas, una vez que sepas hacerlo, te sugiero que revises la parte formal de la programación, la cual es independiente del lenguaje que utilices, y además te hará un mejor programador.
Si tienes alguna duda que no se responde en este documento, por favor plantea tu pregunta para poder responderte. O escribe directamente a soporte@ehack.mx
Referencias
- Por Roberto C. González
Fuente Imágenes
- «Sistema Numérico Hexadecimal»: Imagen cortesía by Nala Systems
- “Conversión Hexadecimal – Binario”: Imagen cortesía by Pexels en Pixabay
Sistema Numérico Hexadecimal, por Roberto C. González. Se distribuye bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.
©2017 - 2025, Ethical Hack, Todos los derechos reservados sobre el contenido propio.