En la lección anterior revisamos los aspectos generales de los arreglos de datos, en esta sección revisaremos temas complementarios que requieren un poco más esfuerzo de usuarios de formación puramente administrativa. Sin embargo espero sea lo suficientemente digerible. Si no es así, deja un comentario para que se pueda mejorar este artículo.
Arreglos Unidimensionales.
Los arreglos que se declaran con un índice, generan lo que denominamos vectores unidimensionales.
TipoDato nombreArreglo [TamañoArreglo];
Como puedes observar es la definición de arreglo que ya revisamos. Es decir, todos los arreglos de la lección anterior son Arreglos unidimensionales. Como ya se dedicó una lección completa a este tipo de arreglos, ya no lo revisaremos en esta sección. Si quieres revisar los arreglos unidimensionales consulta la lección anterior.
Los Arreglos Unidimensionales también reciben en algunas publicaciones el nombre de Vectores y los suelen emplear como sinónimos, esto es cierto en C estándar, pero en C++ aunque esto puede ser discutible (de hecho lo es) pues existen numerosas consideraciones al hablar de vectores, particularmente porque C++ define prototipos y plantillas para Vectores. En esta parte del curso, solo lo dejamos señalado.
Nota: En temas avanzados, C++ implementa los vectores con plantillas, los cuales extienden funcionalidad de los Arreglos estáticos (los que hemos estudiado hasta ahora) en Arreglos dinámicos. Aunque está fuera del alcance de este tutorial, considero necesario que tengas conocimiento de su existencia.
Por no dejar, a continuación un ejercicio de Arreglo Unidimensional o “Vector”. Se omite intencionalmente cualquier comentario. Si tienes alguna duda del código, revisa la lección anterior.
// cpp_48_array03.cpp
// Este programa forma parte del tutorial de introducción al lenguaje C++
// http://a.ehack.info/leguaje-c-introduccion/
// Se ilustra el uso de Arreglos Unidimensionales o Vectores
// 2018, Por http://about.me/carlosgbr
// Versión 1
// Compilado en https://www.onlinegdb.com/online_c++_compiler
#include <iostream>
using namespace std;
int main()
{
const int TamArray = 100;
int valores[TamArray];
float suma = 0, promedio = 0;
cout << "A continuación presentamos el cuadrado del 1 al " << TamArray << endl;
for (int i = 1; i <= TamArray; ++i)
{
if (i<=10) {
cout << i << " - " << i*i << "\t\t";
} else {
cout << i << " - " << i*i << "\t";
}
if (i % 5==0) {
cout << endl;
}
}
cout << "Ahora mostramos el promedio de los cuadrados del 1 al " << TamArray << endl;
for (int i = 1; i <= TamArray; ++i)
{
suma += i*i;
promedio = suma/TamArray;
}
cout << endl;
cout << "El promedio es: " << promedio << "... esto suena a estadística";
return 0;
}
Arreglos Bidimensionales
Las matrices son tipos derivados y, por tanto, pueden construirse a partir de cualquier otro tipo derivado o fundamental, salvo funciones, referencias y void(1). Los Arreglos Bidimensionales cuentan con dos índices en su declaración. Para declarar un Arreglo Bidimensional, utilizamos la siguiente sintaxis.
TipoDato NombreArreglo[TamFila][TamColumna];
en donde,
TipoDato, Tipo de dato que tendrá el arreglo.
NombreArreglo, Identificador que nombra la matriz,
TamFila, número entero que indica cuántas filas existen en la matriz.
TamColumna, número entero que indica cuántas columnas existen en la matriz.
Podrás observar que en utilizamos 2 índices para definir el tamaño del arreglo. De forma intencional se nombraron a los índices TamFila y TamColumna, dado que es posible ver que lo que estamos definiendo lo que en términos algebraicos se denomina una Matriz, aunque puedes nombrarlos como a ti te convenga.
Los Arreglos Bidimensionales se denominan de forma común como Matrices o Tablas.
Considera la siguiente definición de una Matriz:
int Tablero[2][5];
Lo que estamos haciendo con esta declaración, es definir una matriz de 2 filas y 5 columnas. Para mayor claridad puedes visualizar este arreglo de la siguiente forma:
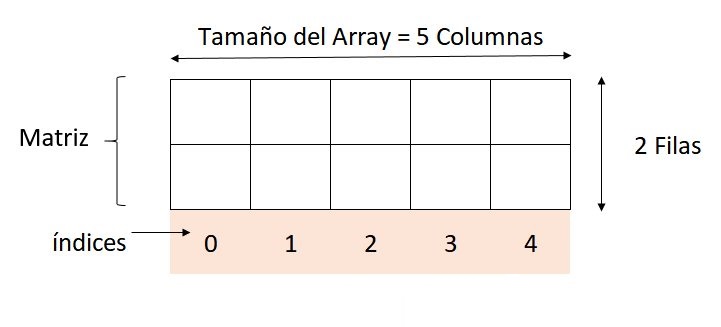
Con esta ilustración es más claro el porqué los arreglos bidimensionales se conocen comúnmente como Matrices. De hecho, ahora te resulta evidente que para realizar el cálculo de matrices algebraicas, los arreglos bidimensionales son las estructuras de datos indicadas para programarlas.
Inicialización de Matrices
La inicialización se puede realizar al declarar una matriz bidimensional de la siguiente forma:
intTablero[2][3] = {{2, 4, 3}, { 4, 5, 6}};
Nota que se agrupan las columnas, el número interno de los corchetes corresponde al número de columnas, el número de grupos corresponde al número de filas. Por claridad de lectura en ocasiones podrás encontrar la matriz anterior con la siguiente notación:
intTablero[2][3] = { {2, 4, 3},
{ 4, 5, 6}};
Esta forma puede ser más clara de identificar.
Sin embargo considera que lo “normal” es asignar los valores de una Matriz en tiempo de ejecución, por lo que en la práctica serán pocas veces que inicialices matrices al declararlas.
Valores predeterminado de matrices bidimensionales (2)
A las matrices se le asignan automáticamente valores iniciales predeterminados a cada uno de sus elementos, de acuerdo a los siguientes criterios:
- Si el tipo del arreglo es numérico, a sus elementos se les asigna el valor cero.
- Si el tipo del arreglo es char, a sus elementos se les asigna el valor ‘\u0000’.
- Si el tipo del arreglo es bool, a sus elementos se les asigna el valor false.
- Si el tipo del arreglo es una clase, a sus elementos se les asigna el valor null.
Ejercicio
Si nunca haz programado el siguiente programa es muy importante, pues muestra el uso de bucles anidados, lo cual en principio puede lucir atemorizarte, solo requiere un poco de paciencia de tu parte. Primero revisemos el código.
// cpp_49_Matriz01.cpp
// Este programa forma parte del tutorial de introducción al lenguaje C++
// http://a.ehack.info/leguaje-c-introduccion/
// Se ilustra el uso de Arreglos Bidimensionales o Matrices
// Se ilustra la inicialización, la captura y el volcado de una Matriz
// 2018, Por http://about.me/carlosgbr
// Versión 1
// Compilado en https://www.onlinegdb.com/online_c++_compiler
#include <iostream>
using namespace std;
int main()
{
const int columna = 2;
const int fila = 3;
int Matriz [columna][fila];
// Inicialización de la matriz, no es estricatamente necesaria, pero se
// utiliza para ilustrar el concepto y los bucles anidados.
for (int i = 0; i < columna; i++) //Con este bucle recorremos las columnas
{
for (int j = 0; j < fila; j++) // Este bucle recorre las filas POR CADA COLUMNA
{
Matriz[i][j] =0;
}
}
cout<<"A continuación se te piden los valores para la Matriz" << endl;
for (int i = 0; i < columna; i++) //Con este bucle recorremos las columnas
{
for (int j = 0; j < fila; j++) // Este bucle recorre las filas POR CADA COLUMNA
{
//Mostramos al usuario en qué posición estamos
cout << "Escribe el valor del elemento [" << i << "][" << j << "]: ";
cin >> Matriz[i][j];
}
}
cout<<"Volcado de la matriz on los datos capturados por el usuario" << endl;
for (int i = 0; i < columna; i++) //Con este bucle recorremos las columnas
{
for (int j = 0; j < fila; j++) // Este bucle recorre las filas POR CADA COLUMNA
{
//Mostramos al usuario el contenido de la matriz.
cout << "[" << i << "][" << j << "]: " << Matriz[i][j] << endl;
}
}
return 0;
}
A continuación puedes ver una posible salida del programa.
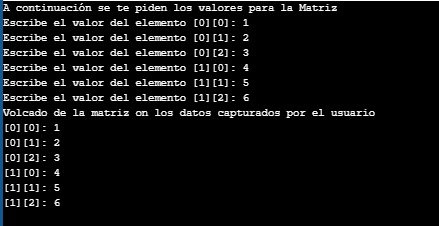
En el código puedes observar varias cosas interesantes:
-
- Utilizamos constantes para definir los límites de la matriz, esto nos permite modificar este valor en un solo punto y no a lo largo de todo el programa.
- Inicialización de la matriz, siempre es conveniente inicializar una estructura de datos (o variable) para evitar comportamientos indeseados.
- Teniendo en mente que una matriz no es otra cosa que una tabla, no resultará muy complicado visualizar como se llenan las matrices. Tomando nuestro ejemplo de 2 filas y 3 columnas:
- Nuestra matriz se define como: Matriz [2][3];
- Para registrar cada elemento se requiere asignar a cada coordenada fila/columna, de acuerdo a nuestro gráfico (considera además que las siguientes líneas son el código “real” que se utilizaría para asignar estos valores a la matriz.):
- Matriz[0][0] = 1;
- Matriz[0][1] = 2;
- Matriz[0][2] = 3;
- Matriz[1][0] = 4;
- Matriz[1][1] = 5;
- Matriz[1][2] = 6;
- Para desplegar esta información (tal como ilustra nuestro ejemplo) utilizaríamos la siguiente salida:
- cout << Matriz[0][0];
- cout << Matriz[0][1];
- cout << Matriz[0][2];
- cout << Matriz[1][0];
- cout << Matriz[1][1];
- cout << Matriz[1][2];
- Considera lo poco práctico que resulta programar de esta forma tanto el despliegue como la captura (e inicialización) de matrices. Considera, Si cambiamos el tamaño de la matriz a, por ejemplo Matriz[50][40]; implicará cambiar el código en varias partes y repetir masivamente instrucciones… con los potenciales problemas que esto implica. Para evitar esta forma de programar el llenado y recuperación de matrices bidimensionales nos valemos de bucles anidados.
- Un bucle anidado lo que hace es fijar una variable, mientras recorre otra. Si te queda claro esto, ya entendiste todo. Considera las sentencias:
for (int i = 0; i < columna; i++) //Con este bucle recorremos las columnas { for (int j = 0; j < fila; j++) // Este bucle recorre las filas POR CADA COLUMNA { /// Proceso, cualquiera } }- for (int i = 0; i < columna; i++) controla la parte del bucle que representa las columnas Matriz[i][]
- Por la forma de operar el bucle for, “esperará” y no cambiará su índice (en este caso i), hasta que las instrucciones internas terminen.
- Dentro del bucle for con índice i, declaramos otro bucle con índice j. Este bucle terminará hasta que se satisfaga la condición j < fila; mientras cambia el bucle i, sigue estático. Por esta situación es que podemos recorrer una matriz con un par de bucles anidados. Lo único importante es que no pierdas de vista la etapa del bucle que estás controlando.
- Mostrar el contenido de la Matriz, no es otra cosa que recorrer nuevamente la matriz, tomar cada par de índices columna/fila y presentar el contenido, nuevamente utilizando un par de bucles anidados.
Es importante que te familiarices y te sientas cómodo usando bucles anidados. Tómate el tiempo para entenderlos, no hay prisa, el tiempo que te quieras “ahorrar” lo tendrás que “pagar con más tiempo ahorrado”. utiliza los ejemplo y haz todos los cambios que se te ocurran, por ejemplo, ¿Cómo implementarías que el usuario determine los límites del Array? ¿Cómo evitarías que se introduzcan valores inválidos? ¿Cómo evitarías que se utilizaran índices fuera de rango? ¿Cómo presentarías los datos en forma de tabla y no lineal?
Aplicación de Matrices
El uso de las matrices casi siempre tienen que ver con áreas matemáticas y afines, así como en la implementación de bases de datos y en la recopilación de grandes volúmenes de datos.(bases de datos).
La manipulación de las mismas se concreta en lo que se ha descrito ya, lo demás que puede parecer “difícil” no tiene que ver con las matrices y su uso en sí, sino en la parte algebraica subyacente y sobre todo en la implementación del algoritmo asociado.
Para ilustrar el uso de matrices en problemas no matemáticos, consideremos un ejemplo simplificado de un juego popular “Batalla naval” (puedes leer acerca de este juego en la Wikipedia), que consiste en adivina la posición de un “barco” para hundirlo.
Programa Batalla naval
La idea general debe considerar lo siguiente:
- El “tablero” de juego (largo y ancho)
- La posición o posiciones del (los) barco(s)
- Solicitar la posición del contrincante.
- Si da una posición que coincida con la posición de nuestro “barco”, lo hunde, sino, no pasa nada (misil desperdiciado!)
- Si “hunde un barco” puede elegir otra posición para lanzar otro “tiro”
- Si falla, cambia el turno al contrincante.
- Gana el primero en hundir la flota del oponente.
El tablero en este caso es una matriz. Las posiciones de los “barcos” se pueden determinar indicando un “B” por ejemplo, el usuario indica una coordenada, y si le atina a uno de nuestros barcos lo hunde, en este caso podemos marcar la casilla con un ‘*’ indicando que lo hemos hundido.
¿Notaste la serie de pasos de 2 párrafos arriba? Es lo que en cómputo se denomina Algoritmo. El cual se puede definir como la serie de pasos lógicos para resolver un problema.
Una aproximación para resolver nuestro simulador de batalla es el siguiente programa:
// cpp_50_Matriz02.cpp
// Este programa forma parte del tutorial de introducción al lenguaje C++
// http://a.ehack.info/leguaje-c-introduccion/
// Se ilustra el uso de Arreglos Bidimensionales o Matrices
// Se implementa una versión simplificada del juego clásico "Batalla naval"
// https://es.wikipedia.org/wiki/Batalla_naval_(juego)
// a partir de la cual se puede extender para mejorar sus prestaciones.
// 2018, Por http://about.me/carlosgbr
// Versión 1
// Compilado en https://www.onlinegdb.com/online_c++_compiler
#include <iostream>
using namespace std;
int main()
{
// Definimos nuestro tablero de 10 x 10 casillas
const int alto =10;
const int ancho = 10;
const int oportunidades = 3;
const char vacio = 'O';
const char barco = 'B';
const char hundido = '*';
char Tablero[alto][ancho];
//char vacio , barco;
int colBarco, filBarco;
//Inicializamos el arreglo con posiciones vacías
for (int i = 0; i < alto; i++) {
for (int j = 0; j < ancho; j++) {
Tablero[i][j] = vacio; // Llenamos de posiciones vacías el Tablero
}
}
// El usuario 1 puede colocar 3 barcos en el Tablero
cout << "Usuario defensor, escribe la posición de tus 3 barcos en el tablero" << endl;
cout << "recuerda que el tablero mide: " << alto << " X " << ancho << " posiciones" << endl << endl;
for (int i = 1; i <= 3; i++){
cout << "Escribe la posición del barco " << i << endl;
cout << "Coordenada X: ";
cin >> colBarco;
cout << "Coordenada Y: ";
cin >> filBarco;
// Nota que restamos 1 a cada valor, revisa el texto.
Tablero[colBarco-1][filBarco-1] = barco;
}
cout << "La posición de tus barcos es" << endl;
for (int i = 0; i < alto; i++){
cout << endl;
for (int j = 0; j < ancho; j++) {
cout << Tablero[i][j] << " ";
}
}
cout << endl << endl << "Listo ya posicionaste tus barcos, ahora daremos en control al atacante" << endl;
// Aquí deberíamos borrar la pantalla, pero aún no revisamos este tipo de función.
// Así que no le damos importancia en este momento.
// Supongamos que el atacante no ve el tablero anterior. Es un buen muchacho :D
cout << endl << "Sr atacante es su oportunidad de hundir los barcos." << endl;
cout << "Cuentas con " << oportunidades << " para hundir los barcos" << endl;
cout << "recuerda que el tablero mide: " << alto << " X " << ancho << " posiciones" << endl << endl;
int i = 0;
do
{
cout << "Escribe la posición del barco " << endl;
cout << "Coordenada X: ";
cin >> colBarco;
colBarco -= 1; // Nota que restamos 1 a cada valor, revisa el texto.
cout << "Coordenada Y: ";
cin >> filBarco;
filBarco -= 1; // Nota que restamos 1 a cada valor, revisa el texto.
//cout << colBarco << ", " << filBarco << endl;
cout << Tablero[colBarco][filBarco] << endl;
if (Tablero[colBarco][filBarco] == barco) {
cout << endl<< "¡¡¡Le diste, barco hundido!!!" << endl << endl << endl;
Tablero[colBarco][filBarco] = hundido;
} else {
cout << endl<< "Más suerte para la próxima" << endl<< endl<< endl;
}
i++;
} while (i < oportunidades);
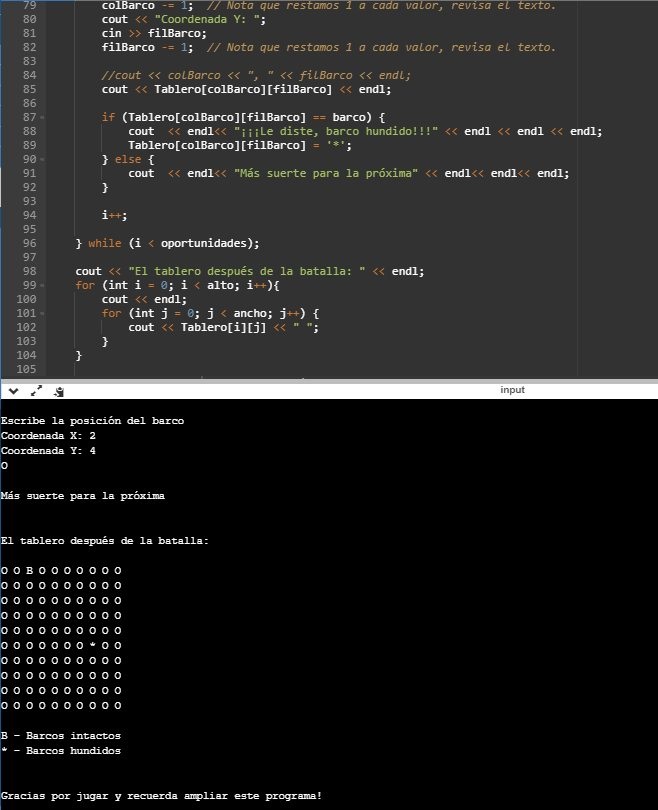
cout << "El tablero después de la batalla: " << endl;
for (int i = 0; i < alto; i++){
cout << endl;
for (int j = 0; j < ancho; j++) {
cout << Tablero[i][j] << " ";
}
}
cout << endl<< endl<< "B - Barcos intactos" << endl;
cout << "* - Barcos hundidos"<< endl<< endl<< endl;
cout << "Gracias por jugar y recuerda ampliar este programa!";
return 0;
}
Hasta ahora este es nuestro programa más extenso, y como puedes comprobar, ya califica en el rango de “ya hace algo”, omitiendo los comentarios y líneas vacías, puedes comprobar que con poco código puedes realizar tareas muy útiles.
Este programa utiliza todo lo que hemos revisando de C++ hasta el momento, desde el uso de constantes para tener un “panel de administración de valores”, estructuras if para validar entradas, estructuras while para controlar el número de repeticiones de los “tiros”, estructuras for tanto para controlar los arreglos bidimensionales como para solicitar las coordenadas de nuestros barcos., además de la implementación del manejo primitivo de una interfaz de usuario.
Revisa el código, todo ya debería quedarte claro. Si tienes alguna duda, revisa las lecciones que correspondan a tu duda o pregunta en los comentarios.
Matrices Multidimensionales
Conceptualmente podemos crear las matrices de cualquier orden que necesitemos, podríamos crear una matriz de 3, 4 o más dimensiones. A partir de 3 dimensiones se vuelve inmanejable el código, al menos en este nivel. Este tipo de matrices tiene sentido en simulaciones y aplicaciones científicas, pues llevan inherentes complejos cálculos.
A modo enunciativos muestro la declaración de una matriz tridimensional.
TipodeDato NombreMatriz[Dim1][Dim2]...[DimN];
en donde,
TipoDato, Tipo de dato que tendrá el arreglo.
NombreArreglo, Identificador que nombra la matriz,
Dim1, número entero que indica el índice de la primera dimensión;
Dim2, número entero que indica el índice de la segunda dimensión;
DimN, número entero que indica el índice de la última dimensión;
A continuación puedes observar una representación gráfica de una matriz de tres dimensiones.
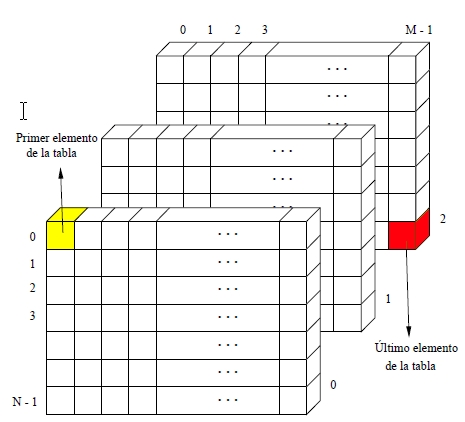
Finalmente se presenta un ejemplo conceptual de una matriz tridimensional. (3)
// cpp_51_Matriz3D.cpp
// Este programa forma parte del tutorial de introducción al lenguaje C++
// http://a.ehack.info/leguaje-c-introduccion/
// Se ilustra el uso de Arreglos Tridimensionales
// Este programa se adaptó del programa localizado en el sitio
// https://www.programiz.com/cpp-programming/multidimensional-arrays
// Por http://about.me/carlosgbr
// Versión 1
// Compilado en https://www.onlinegdb.com/online_c++_compiler
#include <iostream>
using namespace std;
int main()
{
// Este arreglo puede almacenar hasta 12 elementos (2x3x2)
int test[2][3][2];
cout << "Introduce 12 elementos: \n";
// Insertamos los valres en el arreglo test
// utilizando 3 bucles anidados;
for(int i = 0; i < 2; ++i)
{
for (int j = 0; j < 3; ++j)
{
for(int k = 0; k < 2; ++k )
{
cin >> test[i][j][k];
}
}
}
cout<<"\nMostrando los valores:"<<endl;
// Mostrando los valores con el índice apropiado.
for(int i = 0; i < 2; ++i)
{
for (int j = 0; j < 3; ++j)
{
for(int k = 0; k < 2; ++k)
{
cout << "test[" << i << "][" << j << "][" << k << "] = " << test[i][j][k] << endl;
}
}
}
return 0;
}
Conclusión
En ésta y la lección anterior revisamos los arreglos. Aún quedan muchas características que explorar, pero requieren un poco más de conocimientos del lenguaje para logar una comprensión más firme. Por el alcance definido para este curso introductorio, con lo que hemos revisado hasta el momento, es suficiente.
Recuerda que el enfoque de este curso es utilizar herramientas y conceptos que ya se han presentado, esto es la razón que no hemos utilizado muchos recursos que en otros cursos utilizan de forma inmediata. Para este curso prefiero presentar un avance lento, gradual y firme, con la idea de que nadie se quede varado en conceptos que no se han presentado.
Si tienes alguna duda que no se responde en este documento, por favor plantea tu pregunta para poder responderte. O escribe directamente a soporte@ehack.mx
Referencias
- Por Roberto C. González para Ethical Hack
- (1) Matrices en MSDN
- (2) Este párrafo se toma íntegro de Proyecto C++ Universidad Evangelica de El Salvador
- (3) Matriz tridimensional, adaptada del sitio Learn C++
Fuente Imágenes
- «Todas las imágenes de esta sección»: by Nala Systems
Tutorial de C++ by eHack
- Volver al índice de temas del Tutorial de C++
- *** Durante todo este tutorial se repetirá: Este es un curso orientado a gente que nunca ha programado, incluso a gente ajena a la informática. Por esta razón el desarrollo puede parecer lento en ciertas etapas. Prefiero ser claro paso a paso, que hacer “pasos mágicos” como suele ocurrir cuando se enseña programación.
- *** También es buena idea leas esta entrada si te preguntas “Por qué C++”
Código Fuente
- El código fuente de toda la serie lo puedes descargar en nuestro repositorio en github busca los programas con el nombre del encabezado de cada programa.
- Código de esta sección
Arrays en C++ – y II, por Roberto C. González. Se distribuye bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.
©2025, Ethical Hack, Todos los derechos reservados sobre el contenido propio.